什么是幂函数

幂函数是基本初等函数之一，通常表示为 ( y = x^\alpha )，其中 ( \alpha ) 是一个常数，称为指数。幂函数的特点是底数 ( x ) 为自变量，幂 ( \alpha ) 为因变量，指数 ( \alpha ) 为常数。幂函数的图像和性质取决于指数 ( \alpha ) 的值。

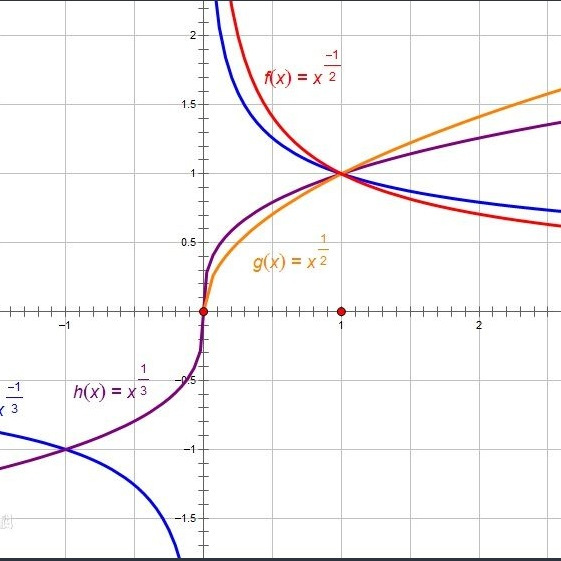
定义域和值域

• 当 ( \alpha > 0 ) 时，幂函数的定义域为 ( [0, +\infty) )，值域为 ( [0, +\infty) )。

• 当 ( \alpha < 0 ) 时，幂函数的定义域为 ( (-\infty, 0) \cup (0, +\infty) )，值域为 ( (0, +\infty) )。

• 当 ( \alpha = 0 ) 时，幂函数的定义域为 ( R \setminus {0} )（即除去0的全体实数集合），值域为 ( {1} )。

奇偶性

• 当 ( \alpha ) 为偶数时，幂函数是偶函数，即图像关于 ( y ) 轴对称。

• 当 ( \alpha ) 为奇数时，幂函数是奇函数，即图像关于原点对称。

单调性

• 当 ( \alpha > 0 ) 时，幂函数在 ( [0, +\infty) ) 区间内是单调递增的。

• 当 ( \alpha < 0 ) 时，幂函数在 ( (0, +\infty) ) 区间内是单调递减的，在 ( (-\infty, 0) ) 区间内是单调递增的。

特殊情况

• 当 ( \alpha ) 为分数时，需要考虑分子和分母的奇偶性来判断函数的性质。

• 当 ( \alpha ) 为负整数时，幂函数的图像在 ( (-\infty, 0) ) 和 ( (0, +\infty) ) 之间，且函数值在 ( x ) 接近0时趋于无穷大，在 ( x ) 接近无穷大时趋于0。

幂函数的图像可以帮助我们更好地理解其性质。例如，当 ( \alpha ) 为正整数时，幂函数的图像是一条平滑的曲线，当 ( \alpha ) 为负整数时，图像是一系列分支，当 ( \alpha ) 为分数时，图像的形状取决于分子和分母的奇偶性。